Homogeneous System Of Linear Equations
Homogeneous system of linear equations. Homogeneous linear differential equations with constant coefficients. We can also solve these solutions using the matrix inversion method. Those systems of two equations and two unknowns only.
Any other solution is a non-trivial solution. This is also true for a linear equation of order one with non-constant coefficients. A 1n x n g 1 x 2 a 21.
A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature which means that the solutions may be expressed in terms of integrals. We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process. Equations 2 3 and 4 constitute a homogeneous system of linear equations in four unknowns.
A system of linear equations is said to be homogeneous if the right hand side of each equation is zero ie each equation in the system has the form a 1x 1 a 2x 2 a nx n 0. The solution to a system of linear inequality is the region where the graphs of all linear inequalities in the system overlap. A A is true and R is the correct explanation of A b A is false and R is not a correrct explanation of A c A is true and R is.
Finding a particular solution to the nonhomogeneous system Ax b. For example is a system of three equations in the three variables x y zA solution to a linear system is an assignment of values to the variables such that all the equations are simultaneously satisfied. Any implicit system which can be divided into system of ODEs which is of the above 4 forms 6.
Therefore for nonhomogeneous equations of the form aybycyrx we already know how to solve the complementary equation and the problem boils down to finding a particular solution for the nonhomogeneous equation. If A. A control system is a system of devices that manages commands directs or regulates the behavior of other devices to achieve a desired result.
Solving the corresponding homogeneous system Ax 0. In such a case given system has infinite solutions.
We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process.
If PAB PA No. C If the system of homogeneous linear equations possesses non-zeronontrivial solutions and Δ 0. Any higher order linear system of ODEs that can be reduced to one of the 5 forms of systems. If PA number of unknowns infinite number of solutions. This returns a basis for the solution space to Ax 0. Do this using the null command by typing nullA. Those systems of two equations and two unknowns only. This is also called trivial solution If PA number of unknowns unique solution. Therefore ρA ρAB 3 4 umber of unknowns.
We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process. A homogeneous system of 3 linear equations in 4 unknowns always has a solution in fact always has a non-trivial solution a solution where the unknowns are not all zero. Where a b and c are constants a 0. And the general form of solutions as. Any other solution is a non-trivial solution. If A. The language and ideas we introduced for first order linear constant coefficient DEs carry forward to the second order casein particular the breakdown into the homogeneous and inhomogeneous cases.

























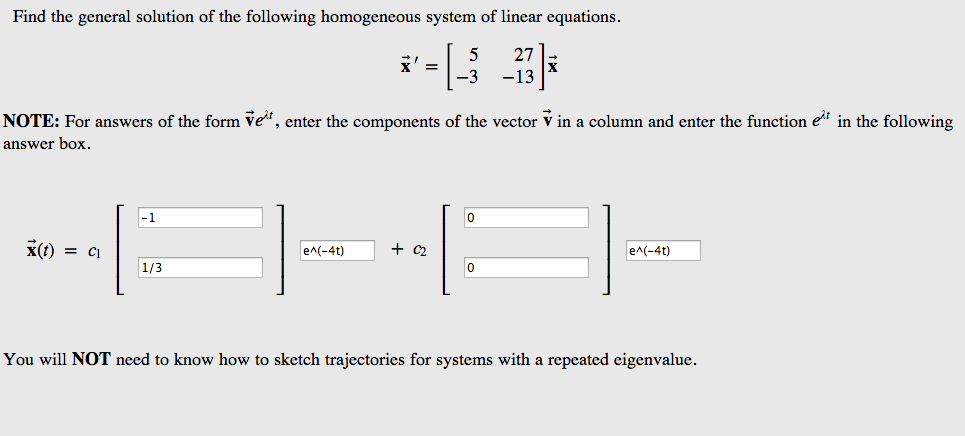



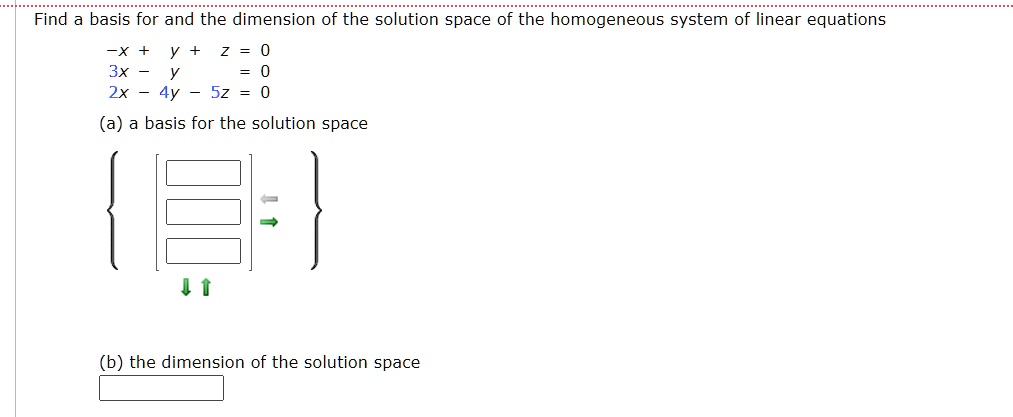


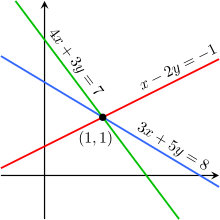













Post a Comment for "Homogeneous System Of Linear Equations"